Gráfica de una ecuación o función cuadrática.
A diferencia de las ecuaciones lineales la gráfica de una ecuación cuadrática es una curva llamada parábola de extensión infinita, cuyo estudio se realiza al considerar la función cudrática o de segundo grado.
Una función cuadrática es una función del tipo,
$$y=ax^2+bx+c~~~~~\mathrm{o}~~~~f(x)=ax^2+bx+c$$
donde \(a,~~b,~~c~~~\in~~\mathbb{R}~~\land~~a\neq0\)
que escrita en forma estándar es,
Forma estándar
$$y=a(x-h)^2+k$$
El punto más alto (o más bajo) es llamado vértice, a continuación, se presentan las principales características de esta gráfica.
Si \(a>0\) abre hacia arriba.
Si \(a < 0\) abre hacia abajo.
El Vértice es el punto \(V\left(h,k\right)\) el cual cumple la relación.
$$V\left(h,k\right)=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)$$
Si \(a< 0\) el vértice \(\left(h,k\right)\) es el punto máximo, si \(a>0\) es mínimo.
Intersecciones: los puntos donde las gráfica de \(ax^2+bx+c=0\) corta los ejes de coordenadas se denominan intersecciones, si hay intersecciones con los ejes quedan determinadas como sigue.
Intersección en eje \(y\),
hacer \(x=0\) en \(ax^2+bx+c=0\) de donde se tiene \(y=c.\)
Intersecciones en eje \(x\), son los
valores que hacen \(ax^2+bx+c=0\) verdadera dentro de \(\mathbb{R}\). Si no existen estos valores la gráfica no interseca el eje de abscisas.
Graficando funciones (ecuaciones) cuadráticas.
Para iniciar note que si se desarrolla la expresión \(y=a(x-h)^2+k\) se llega a la \(y=ax^2+bx+c\) por lo cual todas las consideraciones anteriores aplican para esta expresión también.
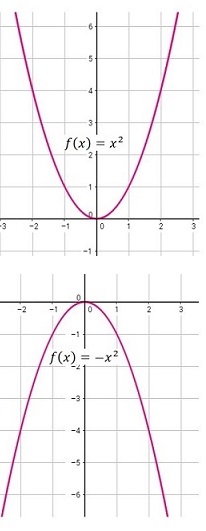Como en toda función, conviene realizar una tabla de valores cuando se va a graficar una ecuación cuadrática, la figura de la izquierda muestra los casos más simples de éstas gráficas. Al estudiar funciones cuadráticas se profundizará en el estudio de estas gráficas.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
Gráficas de ecuacioes cuadráticas
La gráfica de una función cuadrática describe una curva llamada parábola, las cuales se estudian a profundidad al estudiar las secciones cónicas cuya forma es como en la figura siguiente.
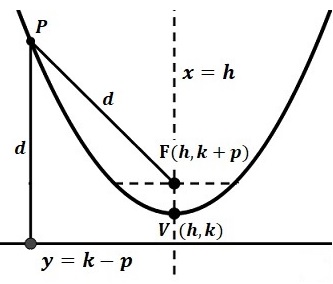
La manera más fácil de realizar una gráfica de cualquier ecuación matemática es utilizar un programa de graficación que sea capaz de mostrar con claridad los detalles de ésta, sin embargo, para la compresión y realización de un buen bosquejo a mano de la gráfica de una ecuación cuadrática, se recomienda conocer un mínimo de cinco o seis puntos por donde pase la gráfica.
Si en \(ax^2+bx+c=0\) el valor \(a\) es positivo la parábola abre hacia arriba (como en la figura) y el vértice \((h,k)\) punto más bajo. Si \(a\) es negativa la parábola abre hacia abajo y el vertice \((h,k)\) es el punto más álto.
Las coordenadas del vértice \((h,k)\) de la parábola quedan determinadas por los valores, \begin{align} \left(h,k\right)&=\left(-\frac{b}{2a},f\left(-\frac{b}{2a}\right)\right)\\ (h,k)&=\left(-\frac{b}{2a},\frac{4ac-b^2}{4a}\right)\end{align} Los punto de cortes (intersecciones) en eje de abscisas (eje \(x\)), si existen son los puntos para los cuales \(ax^2+bx+c=0\) para \( \mathbb{R}\). Si \(ax^2+bx+c=0\) no tiene solución en \(\mathbb{R},\) no hay intersección con el eje \(x.\)
El punto de corte (intersección) con el eje vertical (eje \(y\)), es el punto \((0,c)\) el cual resulta al hacer \(x=0\) en \(ax^2+bx+c=0\).
Otros puntos de la gráfica se obtinen al escribir \(y=ax^2+bx+c,\) darle valores cualquiera a \(x\) y calcular el valor resultante de ye. Para realizar la gráfica basta con unir todos los puntos encontrados con una curva suave.
Como se podrá notar realizar un esbozo de una ecuación cuadrática no conlleva un desafío mayor al de la resolución de la ecuación cuadrática, para esto puede usar el método de su preferencia.
Para más contenidos clic en y luego clic en la pestaña del contenido deseado.
tab-15